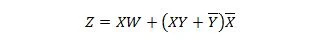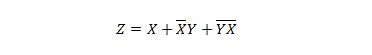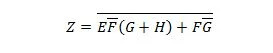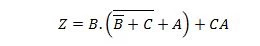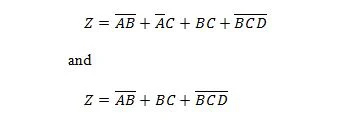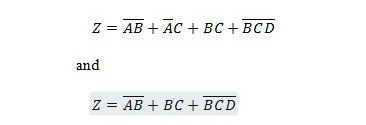2. nodaļa: Būla algebra un ar to saistītās datora sastāvdaļas
2.1. Pamata Būla operatori
Pieņemsim, ka es (autors) esmu garš un jūs (lasītājs) esat garš. Ja kāds jums jautātu, vai mēs abi esam gari, jūs atbildētu “Jā” (patiesība). Ja viņš jautā, vai mēs abi esam īsi, jūs atbildētu “Nē” (nepatiesi). Ja tu esi mazs un es esmu garš, un viņš tev jautā, vai tu vai es esam garš, tava atbilde būtu “Jā” (patiesa). Ja viņš jautā, vai jūs un es esam gari, jums nebūtu atbildes. Jūs varētu turpināt teikt, ka pēdējo jautājumu nevajadzētu uzdot vai ka uz jautājumu nav atbildes. Nu, es vēlos, lai jūs (lasītājs) zinātu, ka šodien noteiktos apstākļos jautājums ir jāuzdod.
Bioloģijā cilvēks ir garš vai īss. Tieši “vides” apstākļi padara cilvēku par vidēju augumu. Viens zinātnieks Džordžs Būls definēja atbilžu vai noteikumu kopumu šāda veida jautājumiem. Šos noteikumus mēs apgūsim šajā tiešsaistes karjeras kursa sadaļā (nodaļā). Šos noteikumus mūsdienās izmanto skaitļošanā, programmēšanā, elektronikā un telekomunikācijās. Patiesībā bez šiem noteikumiem jums nebūtu datora, kā tas ir ierasts mūsdienās; jums nebūtu arī programmēšanas, kā tas ir ierasts mūsdienās.
Patiesība vai meli
Vienkāršs apgalvojums cilvēku valodā pats par sevi ir patiess vai nepatiess. Ja es saku: 'Es esmu garš', tas ir vai nu patiess, vai nepatiess. Ja es saku: “tu esi garš”, tā ir patiesība vai nepatiesa. Ja es esmu garš, bet jūs – maza auguma, un tiek uzdots jautājums, vai gan jūs, gan es esam gari, Būla loģikā ir jāsniedz patiesa vai nepatiesa atbilde. Kuru no šiem diviem vajadzētu dot? Būls īsti neatbildēja uz šo jautājumu. Viņš vienkārši nāca klajā ar noteikumu kopumu, kas mums jāievēro. Labā ziņa ir tā, ka, ievērojot šos noteikumus pareizajā kontekstā, jums nav nekādu neskaidrību. Pateicoties šiem noteikumiem, mums šodien ir datori un programmēšana. Noteikumi jums tagad ir doti. Noteikumus īsti nevar izskaidrot; tu vienkārši pieņem tos. Noteikumi ir trīs sadaļās: UN, VAI un NĒ.
UN
Jautājumu var uzdot, ja gan tu, gan es esam gari. Mans augums un jūsu augums tiek apvienoti ar noteikumu kopumu UN. Šie ir UN noteikumi, kas jāievēro:
nepatiess UN nepatiess = nepatiess
nepatiess UN patiess = nepatiess
patiess UN nepatiess = nepatiess
patiess UN patiess = patiess
Tagad lai lielais ir patiess un īsais ir nepatiess. Tas nozīmē, ka, ja es esmu īss UN tu esi īss, tad tu un es esam īsi. Ja es esmu īss UN tu esi garš, tu un es esam īsi; tā ir Būla atbilde, kas jums jāpieņem. Ja es esmu garš UN tu esi mazs, gan tu, gan es esam īsi. Ja es esmu garš UN tu esi garš, tu un es esam garš. Visi šie ir UN Būla noteikumi, kas jums (lasītājam) vienkārši ir jāpieņem.
VAI
Jautājumu var uzdot, vai tu VAI es esmu garš. Mans augums un jūsu augums tiek apvienoti ar noteikumu kopumu VAI. Šie ir VAI noteikumi, kas jāievēro:
nepatiess VAI nepatiess = nepatiess
nepatiess VAI patiess = patiess
patiess VAI nepatiess = patiess
patiess VAI patiess = patiess
Atkal, lai garš ir patiess un īss ir nepatiess. Tas nozīmē, ka, ja es esmu īss VAI tu esi mazs, tu VAI es esmu īss. Ja es esmu īss VAI tu esi garš, tu vai es esmu garš. Ja es esmu garš VAI tu esi mazs, tu VAI es esmu garš. Ja es esmu garš VAI tu esi garš, tu vai es esmu garš. Visi šie ir Būla noteikumi, kas jums ir jāpieņem.
NAV
Tagad Būla loģikā pastāv tikai divi stāvokļi (iespējamās atbildes). Tas ir, ja jūs NAV garš, jūs esat īss. Ja jūs NAV īss, jūs esat garš; nekas cits. Šie ir NAV noteikumi, kas jāievēro:
NAV nepatiess = patiess
NAV patiess = nepatiess
Pieņemsim, ka jums ir aukla (vai atspere), kuru varat pagarināt (pavilkt). Kamēr virkne ir savā dabiskajā stāvoklī, ja es saku “NAV īsa”, jūs to pagarinātu; tāda ir interpretācija. Kamēr virkne ir pagarināta, ja es saku “NAV gara”, jūs ļautu tai sarauties; tāda ir interpretācija.
Jums ir jāiegaumē visi dotie noteikumi to dažādajās kategorijās.
Vairāk nekā divi operandi
Datorvalodā UN, VAI un NOT katru sauc par operatoru. Lai saņemtu atbildi operatoram NOT, ir nepieciešams tikai viens operands (operatora vērtība). Operatoriem UN vai VAI var būt vairāk nekā divi operandi. Iepriekšējie gadījumi parāda divus operandus UN un VAI. UN var būt trīs operandi, kā norādīts tālāk.
nepatiess UN nepatiess UN nepatiess = nepatiess
nepatiess UN nepatiess UN patiess = nepatiess
Tās ir divas līnijas; katram ir divi UN operatori. Faktiski ir deviņas rindas, kad operandi ir trīs. Izmantojot operatoru UN, tikai pēdējā rinda (devītā rinda) ir vienāda ar patieso; visas iepriekšējās rindas ir nepatiesas. Ņemiet vērā, ka ar diviem operandiem UN tikai pēdējā rinda ir patiesa joprojām; visas iepriekšējās trīs rindas ir nepatiesas. Ja operandi ir četri, ir 16 rindas, un tikai pēdējā rinda ir patiesa operatoram UN.
UN modelis un VAI modelis atšķiras. Ar trim operandiem diviem VAI operatoriem ir arī deviņas rindas, un tikai pirmā rinda šoreiz ir nepatiesa. No otrās līdz devītajai rindai ir taisnība. Ņemiet vērā, ka ar diviem operandiem VAI tikai pirmā rindiņa ir patiesa joprojām; visas atlikušās trīs rindas ir nepatiesas. Ja operandiem VAI ir četri, ir arī 16 rindas.
Operators NOT nodarbojas tikai ar vienu operandu. NAV nepatiess ir patiess un NAV patiess ir nepatiess.
2.2. Divu operandu patiesības tabula un to elektroniskie komponenti
Matemātikā ir tēma, ko sauc par algebru. Neliela daļa no tā bija redzama iepriekšējā nodaļā. Ir sava veida algebra, ko sauc par Būla algebru. Būla algebrā patiesais tiek identificēts ar diviem pamata cipariem, kas ir 1, un false tiek identificēts ar diviem pamata cipariem, kas ir 0.
Iekšējās datora bloka sastāvdaļas ir elektroniskas sastāvdaļas. Datorsistēmas sistēmas vienībā ir digitāli elektroniski komponenti. UN darbību veic neliels elektronisks komponents, ko sauc par UN vārtiem. VAI darbību veic mazais elektroniskais komponents, ko sauc par VAI vārtiem. Darbību NOT veic mazais elektroniskais komponents, ko sauc par NOT vārtiem. Pārāk daudz no šiem vārtiem var būt integrētās shēmas (IC) mikroshēmā.
UN Patiesības tabula un tās vārti
Nākamajā tabulā ir sniegta UN patiesības tabula un tās UN vārtu (mazās ķēdes) simbols:
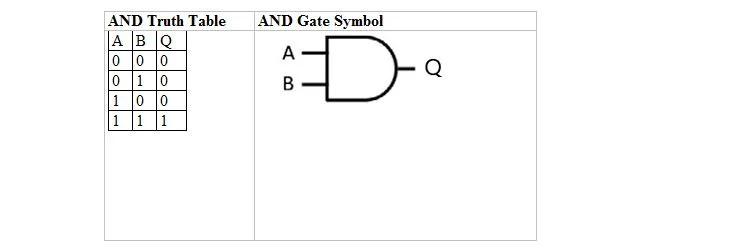
Gan patiesības tabulai UN, gan tās vārtiem A un B ir divi ievades mainīgie. Q ir izejas mainīgais. A ir 1 vai 0. B ir 1 vai 0. Q ir 1 vai 0. UN patiesības tabula ar 1 un 0 ir tāda pati kā iepriekšējais patieso/nepatieso UN patiesības izkārtojums (tabula). UN vienādojums ir:
A . B = Q
kur punkts (.) nozīmē UN (būla). Punktu var izlaist, lai būtu AB = Q, kas nozīmē to pašu (UN).
Piezīme: A un B biti četrās rindās kā pāri ir pirmie četri skaitļi otrajā bāzē, sākot no 0 (vai 00), t.i., 00, 01, 10, 11.
Nākamajā tabulā ir parādīta VAI patiesības tabula un tās VAI vārtu (mazās ķēdes) simbols:
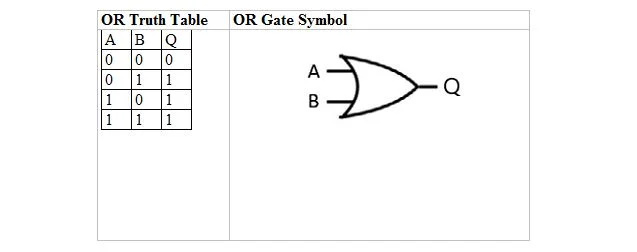
Gan VAI patiesības tabulai, gan tās vārtiem A un B ir divi ievades mainīgie. Q ir izejas mainīgais. VAI patiesības tabula ar 1 un 0 ir tāda pati kā iepriekšējais patiesās/nepatiesās VAI patiesības izkārtojums (tabula).
VAI vienādojums ir:
A + B = Q
Kur + šeit nozīmē Būla VAI, nevis pievienošanu. Vienādojums tiek lasīts kā 'A vai B vienāds ar Q'.
Nākamajā tabulā ir sniegta NAV patiesības tabula un tās NAV vārti (mazās ķēdes) simbols:
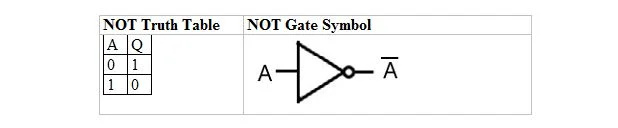
NOT patiesības tabulai vai NOT vārtiem ir tikai viena ieeja un viena izeja. Kad ieeja ir 0, izvade ir 1. Ja ievade ir 1, izvade ir 0. NOT vārti veic sava veida inversiju. Izvades mainīgais ir tāds pats kā ievades mainīgais, bet ar joslu (pārklāta). NAV patiesības tabula ar 1 un 0 ir tāda pati kā iepriekšējais patieso/nepatieso VAI patiesības izkārtojums (tabula).
NOT vienādojums ir:
A = Q
Kur Q = A un josla virs A šeit nozīmē papildinājumu. Papildinājums 0 ir 1 un papildinājums 1 ir 0. NOT vārti ir pazīstami arī kā INVERTING vārti.
Šīs ir fundamentālās (vai saknes) patiesības tabulas un to vārti (mazās shēmas) digitālajā elektronikā (ar Būla algebru). Pārējās trīs patiesības tabulas, kas ir norādītas nākamajā ilustrācijā, un to vārti ir paredzētas ērtībai, un to pamatā ir trīs iepriekšējās patiesības tabulas.
Ir patiesības tabula un vārti, kas ir atvasināti no UN patiesības tabulas un vārtiem. Tos sauc par NAND (for NOT AND) patiesības tabulu un atbilstošo NAND vārti. NAND patiesības tabula un tās NAND vārti ir:
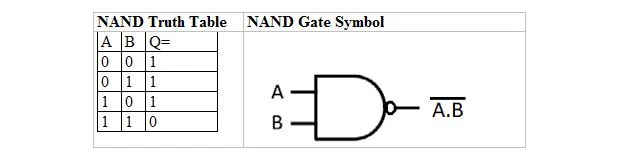
Lai iegūtu NAND patiesības tabulu, dodieties uz UN patiesības tabulas izvadi un aizstājiet katru ciparu ar tā papildinājumu. Papildinājums 0 ir 1 un papildinājums 1 ir 0. NAND vārti ir līdzīgi vārtiem UN, bet pirms izvadlīnijas ir mazs aplis. NAND vienādojums ir:
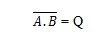
Kur nozīmē “A” UN “B” rezultāta papildinājumu. Joslu (virslīniju) vārtos attēlo mazais aplis. Ņemiet vērā, ka punktu starp A un B var izlaist.
Ir vēl viena patiesības tabula un vārti, kas ir atvasināti no VAI patiesības tabulas un vārtiem. Tos sauc par NOR (for NOT OR) patiesības tabulu un atbilstošo NOR vārti. NOR patiesības tabula un tās NOR vārti ir:
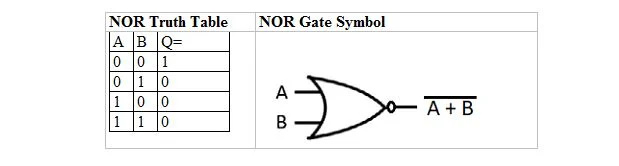
Lai iegūtu NOR patiesības tabulu, dodieties uz VAI patiesības tabulas izvadi un aizstājiet katru ciparu ar tā papildinājumu. Papildinājums 0 ir 1 un papildinājums 1 ir 0. NOR vārti ir līdzīgi VAI vārtiem, bet tiem ir mazs aplis pirms izvadlīnijas. NOR vienādojums ir:
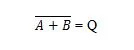
Kur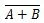 
nozīmē “A” VAI “B” rezultāta papildinājumu. Joslu (virslīniju) vārtos attēlo mazais aplis.
Ekskluzīvs VAI (XOR)
VAI vārtu patiesības tabula ir šāda:
Parastā angļu valodā nav skaidrs, vai pēdējai rindai 1 VAI 1 ir jādod 1 vai 0. Tātad Būla algebrā ir divu veidu VAI patiesības tabulas un divi atbilstoši vārti. Izmantojot parasto VAI, pēdējā rinda 1 VAI 1 dod 1. Cits VAI veids ir ekskluzīvais VAI (XOR), kur pirmās trīs rindas ir tādas pašas kā pirmās trīs parastā VAI rindas (ieskaitot izvadi). Tomēr ceturtajā un pēdējā rindā 1 VAI 1 dod 0.
Nākamajā tabulā ir sniegta XOR patiesības tabula un tās XOR vārtu (mazās ķēdes) simbols:
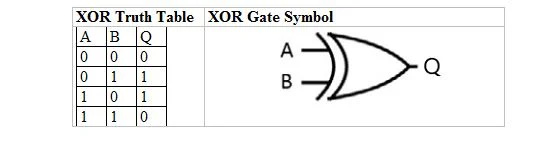
Gan XOR patiesības tabulai, gan tās vārtiem “A”, kā arī “B” ir divi ievades mainīgie. “Q” ir izvades mainīgais.
XOR vienādojums ir:
A ⊕ B = Q
Kur ⊕ šeit nozīmē Būla XOR.
Parastais VAI nozīmē vienu vai abus. Ekskluzīvs VAI nozīmē stingri arī un ne abi.
2.3 Būla postulāti
Postulāti ir pieņēmumi, pamatojoties uz kuriem tiek izdarīti noteikti secinājumi. Ir desmit Būla postulāti, kas sakņojas no vienādojumiem UN, VAI un NOT (patiesības tabulas). Šos vienādojumus sauc arī par funkcijām. Pamatfunkcijas tiek pārkopētas šādi:
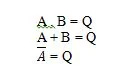
Šīs ir Būla algebras pamatfunkcijas (vienādojumi). Pārējie trīs (funkciju) vienādojumi nav pamatfunkcijas:
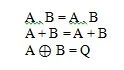
Lai gan pēdējā funkcija šeit ir savdabīga, tā netiek uzskatīta par pamatfunkciju.
Būla postulāti ir šādi:
No UN funkcijas
1) 0. 0 = 0
divdesmit . 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
No funkcijas VAI
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
No NOT Function
9) 0 = 1
10) 1 = 0
Piezīme: Šie postulāti ir tikai rindas UN, VAI un NOT patiesības tabulās, kas izteiktas neatkarīgi. Lasītājam jāiegaumē dotie postulāti.
2.4 Būla rekvizīti
Īpašums ir kā kaut kā īpašība. Būla īpašības ir vienādojumi, kas iegūti no Būla postulātiem. Šajā sadaļā rekvizīti ir vienkārši norādīti bez to atvasinājumiem un pēc tam tiek izmantoti. Ir divdesmit pieci rekvizīti, kas ir sagrupēti zem desmit virsrakstiem šādi:
Funkcijas UN īpašības
1. īpašums:
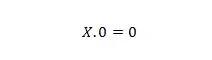
Kur X var būt 1 vai 0. Tas nozīmē, ka neatkarīgi no tā, kas ir X, rezultāts vienmēr ir 0.
Piezīme. Mainīgajam nav obligāti jābūt A vai B, vai C vai D. Mainīgais var būt W vai X, Y vai Z vai jebkurš cits burts.
2. īpašums:
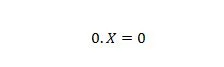
Kur X var būt 1 vai 0. Ņemiet vērā, ka atšķirība starp īpašību 1 un īpašību 2 ir tāda, ka abu vienādojumu vienādības zīmes kreisajā pusē X un 0 pozīcijas tiek apmainītas.
3. īpašums:
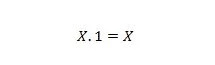
Ja X ir 0, tad 0. 1 = 0. Ja X ir 1, tad 1. 1 = 1.
4. īpašums:
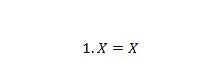
Ja X ir 0, tad 1. 0 = 0. Ja X ir 1, tad 1. 1 = 1. Ņemiet vērā, ka atšķirība starp īpašību 3 un īpašību 4 ir tāda, ka abu vienādojumu kreisajā pusē atrodas X un 1 ir apmainīti.
Funkcijas VAI īpašības
5. īpašums:
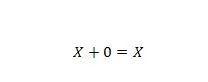
Kur X var būt 1 vai 0. Tas nozīmē, ka, ja X ir 0, rezultāts ir 0. Ja X ir 1, rezultāts ir 1.
6. īpašums:
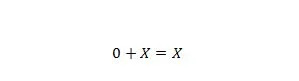
Kur X var būt 1 vai 0. Ņemiet vērā, ka atšķirība starp īpašību 5 un īpašību 6 ir tāda, ka abu vienādojumu kreisajā pusē X un 0 pozīcijas tiek apmainītas.
7. īpašums:
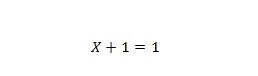
Ja X ir 0, tad 0 + 1 = 1. Ja X ir 1, tad 1 + 1 = 1.
8. īpašums:
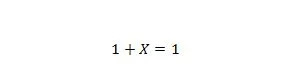
Ja X ir 0, tad 1 + 0 = 1. Ja X ir 1, tad 1 + 1 = 1. Ņemiet vērā, ka atšķirība starp īpašību 7 un īpašību 8 ir tāda, ka abu vienādojumu kreisajā pusē atrodas X un 1 ir apmainīti.
Īpašības, kas attiecas uz mainīgā lieluma kombināciju ar sevi vai tā papildinājumu
9. īpašums: 
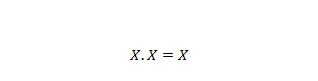
Tas ir: ja X ir 0, tad 0 . 0 = 0. Ja X ir 1, tad 1 . 1 = 1.
10. īpašums:
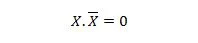
Tas ir: ja X ir 0, tad 0. 1 = 0. Ja X ir 1, tad 1. 0 = 0.
Secīgiem mainīgajiem šis īpašums kļūst:
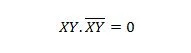
11. īpašums:
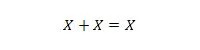
Tas ir: ja X ir 0, tad 0 + 0 = 0. Ja X ir 1, tad 1 + 1 = 1 (no parastā VAI).
12. īpašums:
Tas ir: ja X ir 0, tad 0 + 1 = 1. Ja X = 1, tad 1 + 0 = 1.
Tas ir: ja X ir 0, tad 0 + 1 = 1. Ja X = 1, tad 1 + 0 = 1.
Dubultā papildināšana
13. īpašums:
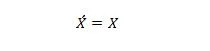
Ja X kreisajā pusē ir 0, X labajā pusē kļūst par 0. Ja X labajā pusē ir 1, X kreisajā pusē kļūst par 1. Citiem vārdiem sakot, dubultie papildinājumi atgriež sākotnējo vērtību.
Komutatīvais likums
14. īpašums:
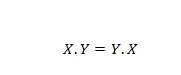
Tas nozīmē, ka pirmā un otrā operanda apmaiņai ar operatoru UN vienādības zīmes kreisajā pusē nav nozīmes; atbilde joprojām ir tāda pati pēc tam, kad ir notikusi apmaiņa kreisajā pusē. Šo vienādojumu var uzrakstīt, izlaižot punktus: XY = YX.
15. īpašums:
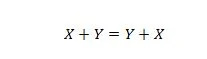
Paskaidrojums šeit ir tāds pats kā iepriekšējā UN, bet tas ir paredzēts operatoram VAI.
Sadales likums
16. īpašums:
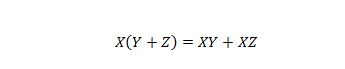
Šeit ir trīs mainīgie: X, Y un Z. Katrs mainīgais var būt 1 vai 0. Vienādības simbola kreisajā pusē iekavas nozīmē vispirms novērtēt, kas tajos ir. Tad UN ir rezultāts ar X. Labajā pusē ir teikts, ka X UN Y kopā VAI X UN Z kopā ir tas pats, kas kreisajā pusē. Ņemiet vērā, ka UN punktu operators ir pilnībā izlaists; un apvienotie mainīgie joprojām nozīmē UN.
17. īpašums:
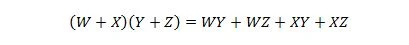
Šis rekvizīts ir rekvizīta 16 paplašinājums ar pievienotu mainīgo W.
Asociatīvās tiesības
18. īpašums:
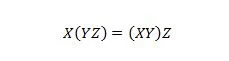
Iekavas nozīmē vispirms novērtēt to, kas ir iekavās. Tātad, izteiksmei kreisajā pusē, ja Y ar Z vispirms ir UN un X ir UN ar rezultātu, tad gala rezultāts kreisajā pusē ir tāds pats kā gala rezultāts labajā pusē. -rokas puse, kur X ar Y ir UN pirms rezultāta UN pievienošanas ar Z. Ņemiet vērā, ka vienādojumā punkti ir izlaisti.
Īpašums 19:
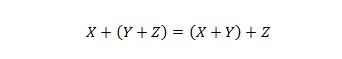
Šis rekvizīts ir izskaidrots līdzīgi kā rekvizīts 18, taču operatora UN vietā tiek izmantots operators VAI. Operators VAI nekad netiek izlaists Būla izteiksmē vienkāršības labad. No otras puses, operatoru UN var izlaist un abus mainīgos var apvienot.
Absorbcija
Īpašums 20:
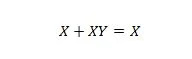
Izmantojot šo vienādojumu, neatkarīgi no tā, kas ir Y, labā puse vienmēr būs X (absorbēta).
Īpašums 21:
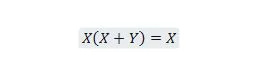
Turklāt ar šo vienādojumu neatkarīgi no tā, kas ir Y, labā puse vienmēr būs X (absorbēta). Šis rekvizīts 21 ir tāds pats kā rekvizīts 20, kas ir:
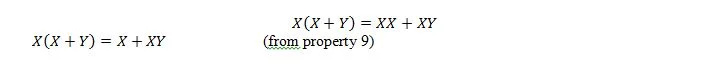
Šeit mēs izmantojam sadales likumu un faktu, ka X.X = X īpašuma 9.
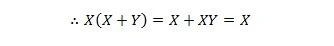
Identitāte
Īpašums 22:
Tas nozīmē, ka X + Y izteiksmei X papildinājums Y priekšā nemaina izteiksmi.
Īpašums 23:
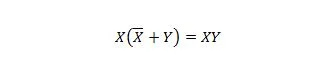
Tas nozīmē, ka XY izteiksmei X ORed papildinājums ar Y iekavās, kas tiek darīts vispirms, nemaina XY izteiksmi.
DeMorgana likums
Īpašums 24:
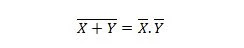
Tas nozīmē, ka NOR (NOT OR) vārtiem ir tāds pats rezultāts, kā ATZĪMĒT abas ievades pirms UN to ievadīšanas.
Īpašums 25:
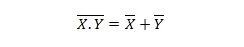
Tas nozīmē, ka NAND (NOT AND) vārtiem ir tāds pats rezultāts kā ATZĪMĒŠANAI abām ieejām pirms VAI.
Sniegtās ilustrācijas ir 25 rekvizīti. Tos var pierādīt, aizvietojot visas dažādās iespējamās 1 un 0 vērtības katrā izteiksmē kreisajā pusē, lai redzētu, vai ir iegūta izteiksme (vai rezultāts) labajā pusē. Pierādījumi tiek atstāti kā uzdevums lasītājam.
2.5. Salikto izteiksmju vienkāršošana
Šīs divas funkcijas ir vienādas:
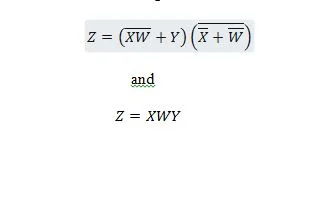
Z ir izeja un X, W un Y ir ieejas. Pirmajam ir nepieciešami NAND vārti, VAI vārti, UN vārti, divi NAV vārti, VAI vārti un NOR vārti. Otrajam nepieciešami tikai divi UN vārti. Pirmais ir vienādojums ar saliktu izteiksmi labajā pusē, kas ir vienkāršots (samazināts) līdz otrajam vienādojumam vienam labās puses izteiksmes vienumam.
Vienkāršošana vai samazināšana noved pie mazāka vārtu skaita, lai īstenotu to pašu funkciju kā ķēde. Šāda mazāka shēma var būt daļa no integrētās shēmas (IC) vai būt atsevišķa shēma datora mātesplates virsmā.
Kad funkcija (vienādojums) nonāk projektēšanas procesā, ir jāveic vienkāršošana, lai samazinātu vārtu skaitu un iegūtu lētāku shēmu. Vienkāršošanai nepieciešams izmantot vienu vai vairākus no iepriekšējiem divdesmit pieciem Būla rekvizītiem.
2.51. piemērs:
Samaziniet vienādojumu:
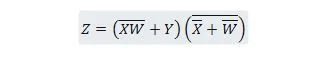
Piezīme: Divas iekavas blakus viena otrai nozīmē, ka iekavas ir UN (punkts starp tām pēc izvēles nav rakstīts).
Risinājums:
Risinājumiem katra soļa pamatojums (iemesls) dots soļa labajā pusē, iekavās. Lasītājam jāizlasa katrs solis un tā pamatojums. Lasītājam ir jāatsaucas arī uz iepriekšējiem rekvizītiem, kad viņš/viņa lasa funkciju samazināšanas soļus.
2.52. piemērs:
Vienkāršot:
2.6. Minimālā produktu summa
Šīs divas funkcijas ir vienādas:
Tiek uzskatīts, ka abu vienādojumu abas labās puses izteiksmes ir produktu summas (SP) formā. Tiek uzskatīts, ka izteikta izteiksme atrodas veidlapā Produktu summa, ja tai nav iekavas. Ir skaidrs, ka pirmajai funkcijai (vienādojumam) ir nepieciešams vairāk vārtu nekā otrajai funkcijai.
Pirmo labās puses izteiksmi joprojām var samazināt, lai iegūtu otro funkciju. Otro labās puses izteiksmi nevar vēl vairāk vienkāršot, un to joprojām var izteikt kā produktu summu (terminu “papildinājums”). Otro labās puses izteicienu īsti vairs nevar vienkāršot. Tātad tiek teikts, ka tas ir minimālās produktu summas (MSP) formā.
2.61. piemērs:
Vispirms ievadiet šo funkciju veidlapā Produktu summa un pēc tam uz veidlapu Minimālā produktu summa.
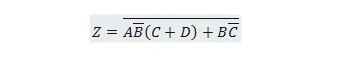
Risinājums:
Risinot šādas problēmas, ir jāizmanto viens vai vairāki no iepriekšējiem divdesmit pieciem rekvizītiem, kā parādīts šajā risinājumā:
2.6. Minimālā produktu summa
Šīs divas funkcijas ir vienādas:
Tiek uzskatīts, ka abu vienādojumu abas labās puses izteiksmes ir produktu summas (SP) formā. Tiek uzskatīts, ka izteikta izteiksme atrodas veidlapā Produktu summa, ja tai nav iekavas. Ir skaidrs, ka pirmajai funkcijai (vienādojumam) ir nepieciešams vairāk vārtu nekā otrajai funkcijai.
Pirmo labās puses izteiksmi joprojām var samazināt, lai iegūtu otro funkciju. Otro labās puses izteiksmi nevar vēl vairāk vienkāršot, un to joprojām var izteikt kā produktu summu (terminu “papildinājums”). Otro labās puses izteicienu īsti vairs nevar vienkāršot. Tātad tiek teikts, ka tas ir minimālās produktu summas (MSP) formā.
2.61. piemērs:
Vispirms ievadiet šo funkciju veidlapā Produktu summa un pēc tam uz veidlapu Minimālā produktu summa.
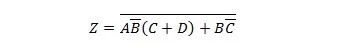
Risinājums:
Risinot šādas problēmas, ir jāizmanto viens vai vairāki no iepriekšējiem divdesmit pieciem rekvizītiem, kā parādīts šajā risinājumā:
Šī pēdējā izteiksme ir veidlapā Produktu summa (SP), bet ne veidlapā Minimālā produktu summa (MSP). Uz jautājuma pirmo daļu ir sniegta atbilde. Otrās daļas risinājums ir šāds:
Šī pēdējā vienkāršotā funkcija (vienādojums) ir MSP formā, un tās ieviešanai ir nepieciešams mazāks vārtu skaits nekā tai atbilstošajai SP formai. Atcerieties: SP nozīmē produktu summu, savukārt MSP nozīmē minimālo produktu summu.
2.62. piemērs:
Nākamajā ķēdē ir X, Y un W ieejas, un Z ir izeja. Izveidojiet produktu summas (SP) funkciju (šķietamā minimālās produktu summas funkciju) Z. Pēc tam izveidojiet patieso, vairāk samazinātu (minimizētu) produktu summu (MSP). Pēc tam ieviesiet MSP ķēdi (uzzīmējiet MSP vārtu tīklu).
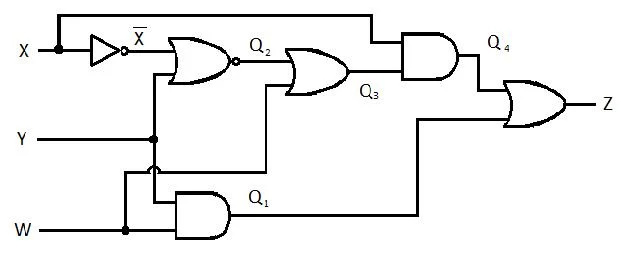
2.61. att. A bloķēšanas ķēde
Risinājums:
Pirms vienkāršošanas procesa sākšanas Z izteiksme ir jāiegūst X, Y un W izteiksmē. Skatiet šo diagrammas ilustrācijas piemēru:
Šī ir Z izteiksme X, Y un W izteiksmē. Pēc tam var notikt vienkāršošana uz šķietamo MSP. Šķietamais MSP ir SP.
Šis pēdējais vienādojums (funkcija) ir SP formā. Tā nav taisnība Minimālā produktu summa (vēl nav MSP). Tātad samazināšana (minimizācija) ir jāturpina.
Šis pēdējais vienādojums (funkcija) ir patiesa minimālā produktu summa (MSP). Minimālās produktu summas (patiesā minimizēšanas) vārstu ķēde ir:
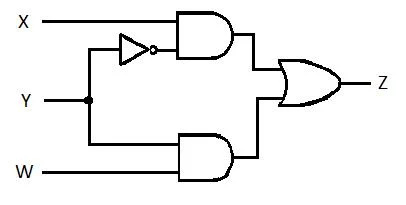
2.62. att. MSP vārstu ķēde
komentēt
No šīs sadaļas analīzes var redzēt, ka nav skaidrs, vai produktu summa ir minimālā produktu summa vai nē. SP nav īpaši noderīgs. Tas ir MSP, kas ir ļoti noderīgs. Ir drošs veids, kā iegūt JTP; tas ir izmantot Karnaugh karti. Karnaugh Map ir ārpus šī tiešsaistes karjeras kursa darbības jomas.
2.7 Problēmas
Pirms pāriet uz nākamo nodaļu lasītājam ir ieteicams atrisināt visas nodaļas problēmas.
- Izveidojiet UN, VAI un NOT patiesības tabulas ar tām atbilstošajiem vārtiem.
- Pierakstiet desmit Būla postulātus dažādās kategorijās, nosaucot kategorijas.
- Bez paskaidrojumiem pierakstiet divdesmit sešas Būla algebras īpašības dažādās kategorijās, nosaucot kategorijas.
- Samaziniet vienādojumu, izmantojot Būla īpašības un citējot izmantotās kategorijas.
- Samaziniet vienādojumu, izmantojot Būla īpašības un citējot izmantotās kategorijas.
- Izmantojot Būla rekvizītus un citējot izmantotās kategorijas, samaziniet šādu vienādojumu — vispirms uz produktu summu un pēc tam uz minimālo produktu summu:
- Izmantojot Būla rekvizītus un citējot izmantotās kategorijas, samaziniet šādu vienādojumu — vispirms uz produktu summu un pēc tam uz minimālo produktu summu:
