Lielu vektoru reizinājuma aprēķināšana nav viegls uzdevums. Tas var prasīt lielus aprēķinus un laiku, aprēķinot to manuāli. Tomēr mūsdienu augsto skaitļošanas rīku laikmetā mēs esam svētīti ar MATLAB, kas veic daudzus aprēķinus pēc iespējas īsākā laikā, izmantojot iebūvētās funkcijas. Viena no šādām funkcijām ir krusts () kas ļauj noteikt divu vektoru krustreizinājumu.
Šī apmācība atklās:
- Kas ir krusteniskais produkts?
- Kāpēc mums ir jānosaka Cross produkts?
- Kā MATLAB noteikt divu vektoru krustojumu?
- Piemēri
- Secinājums
Kas ir krusteniskais produkts?
The šķērsprodukts no diviem vektoriem ir fizisks lielums, ko aprēķina, reizinot divus vektorus. Tas atgriež vektoru perpendikulāri uz dotajiem diviem vektoriem. Ja A un B ir divi vektoru lielumi, to šķērsprodukts C ir norādīts kā:
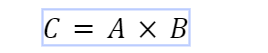
Kur C ir arī vektora lielums, un tas ir perpendikulārs abiem A un B .
Kāpēc mums ir jānosaka Cross produkts?
The šķērsprodukts veic daudzus uzdevumus fizikā, matemātikā un inženierzinātnēs. Daži no tiem ir norādīti zemāk.
The šķērsprodukts tiek izmantots, lai atrastu:
- Trijstūra laukums.
- Leņķis starp diviem vektoriem.
- Vienības vektors, kas ir perpendikulārs diviem vektoriem.
- Paralelograma laukums.
- Divu vektoru kolinearitāte.
Kā MATLAB ieviest divu vektoru krustojumu?
MATLAB atvieglo mūs ar iebūvētu krusts () funkcija, lai atrastu krusta produkts no diviem vektoriem. Šī funkcija pieņem divus vektorus kā obligātus ievades datus un nodrošina tos krusteniskā ražošana t vektora daudzuma izteiksmē.
Sintakse
The krusts () Funkciju var ieviest MATLAB, izmantojot norādītos veidus:
C = krusts ( A, B )C = krusts ( A, B, blāvs )
Šeit,
Funkcija C = krusts(A,B) ir atbildīgs par aprēķinu krusteniskais produkts C no dotajiem vektoriem A un B .
- Ja A un B attēlo vektorus, tiem jābūt a Izmērs vienāds ar 3 .
- Ja A un B apzīmē divas matricas vai daudzvirzienu masīvus, tiem jābūt vienāda izmēra. Šajā situācijā, krusts () funkcija uzskata A un B kā vektoru kolekciju ar trim elementiem un aprēķina tos krusta produkts gar pirmo izmēru, kura izmērs ir vienāds ar 3.
Funkcija C = krusts (A, B, blāvs) ir atbildīgs par aprēķinu krusteniskais produkts C no dotajiem diviem masīviem A un B gar dimensijas dim . Paturiet to prātā A un B jābūt diviem masīviem ar vienādu izmēru un izmērs (A, dim) , un izmērs (B, dim) jābūt vienādam ar 3 . Šeit, blāvs ir mainīgais, kas satur pozitīvu skalāro lielumu.
Piemēri
Apsveriet dažus piemērus, lai saprastu praktisko īstenošanu krusts () funkcija MATLAB.
1. piemērs. Kā noteikt divu vektoru krustojumu?
Šajā piemērā mēs aprēķinām šķērsprodukts C no dotajiem vektoriem un izmantojot krusts () funkciju.
A = [ - 7 9 2.78 ] ;B = [ 1 0 - 7 ] ;
C = krusts ( A, B )

Tagad mēs varam pārbaudīt savu rezultātu C paņemot to punktu produkts ar vektoriem A un B. Ja C ir perpendikulāri uz abiem vektoriem A un B tas nozīmē C ir krusta produkts no A un B . Mēs varam pārbaudīt perpendikularitāte no C ar A un B paņemot to punktu produkts ar A un B . Ja punktu produkts no C ar A un B vienāds 0. tas nozīmē C ir perpendikulāri uz A un B .
punkts ( C,A ) == 0 && punkts ( C, B ) == 0Pēc iepriekš minētā izpildes perpendikulitātes tests, mēs ieguvām a loģiskā vērtība 1 tas nozīmē, ka iepriekš minētā darbība ir patiesa. Tādējādi mēs secinām, ka rezultējošais vektors C pārstāv šķērsprodukts no dotajiem vektoriem A un B .

2. piemērs. Kā noteikt divu matricu krustojumu?
Dotais piemērs aprēķina šķērsprodukts C no dotajām matricām A, izveidots, izmantojot funkciju magic() un B , nejaušu skaitļu matrica, izmantojot krusts () funkciju. Abas matricas A un B ir vienāda izmēra.
A = maģija ( 3 ) ;B = rand ( 3 , 3 ) ;
C = krusts ( A, B )
Rezultātā iegūstam a 3 pa 3 matrica C tas ir šķērsprodukts no A un B . Katra kolonna no C pārstāv krusta produkts attiecīgajām kolonnām A un B . Piemēram, C(:,1) ir krusta produkts no A(:,1) un B(:,1) .

3. piemērs. Kā atrast divu daudzvirzienu masīvu šķērsproduktu?
Dotais MATLAB kods nosaka šķērsprodukts C no dotajiem daudzvirzienu masīviem A , nejaušu veselu skaitļu masīvs un B , nejaušu skaitļu masīvs, izmantojot krusts () funkciju. Abi masīvi A un B ir vienāda izmēra.
A = randi ( 100 , 3 , 4 , 2 ) ;B = randn ( 3 , 4 , 2 ) ;
C = krusts ( A, B )
Rezultātā iegūstam a 3 reiz 4 reizes masīvs C tas ir šķērsprodukts no A un B. Katra kolonna no C pārstāv krusta produkts attiecīgajām kolonnām A un B . Piemēram, C(:,1,1) ir krustojums A(:,1,1) un B(:,1,1) .

4. piemērs. Kā atrast divu daudzvirzienu masīvu šķērsproduktu norādītajā dimensijā?
Apsveriet masīvus A un B no 3. piemērs kam ir izmērs 3 reizes 3 reizes un izmantojiet krusts () funkcija, lai to atrastu krusta produkts līdzi izmērs dim=2 .
A = randi ( 100 , 3 , 3 , 3 ) ;B = randn ( 3 , 3 , 3 ) ;
C = krusts ( A, B, 2 )
Rezultātā iegūstam a 3 reizes 3 reizes masīvs C tas ir šķērsprodukts no A un B . Katra rinda no C apzīmē attiecīgo rindu šķērsreizinājumu A un B. Piemēram, C(1,,1) ir krustojums A(1,:,1) un B(1,:,1) .

Secinājums
Meklējot krusta produkts Divu vektoru darbība ir izplatīta darbība, ko plaši izmanto matemātikas un inženierijas uzdevumos. Šo darbību var veikt MATLAB, izmantojot iebūvēto krusts () funkciju. Šajā rokasgrāmatā ir izskaidroti dažādi veidi, kā ieviest šķērsprodukts MATLAB, izmantojot vairākus piemērus.